Determinant of a Sparse Matrix

• Project Type: Algorithm, Data Structures
• Tools Used: Java
• Project Goals:
  • Create a sparse matrix that only stores non-zero values.
  • Using the sparse matrix, recursively find the determinant of the matrix.

1. Understanding the Problem Statement

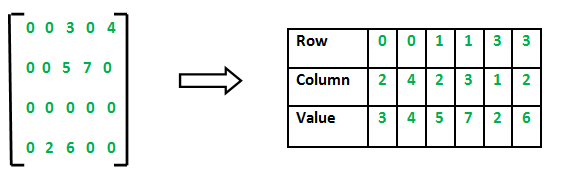
The goal was to compute the determinant of an NxN sparse matrix, meaning a matrix where most elements are zero. Instead of storing the entire matrix in memory, the program only stored non-zero values using an efficient data structure.

2. Choosing a Data Structure

Since the matrix is sparse, a compact storage solution was required. The approach taken:

• Used a two-dimensional data structure:
  • The first dimension was an array that indexed rows.
  • The second dimension was a stack that stored column indices along with their corresponding non-zero values.
• This design ensured memory efficiency by avoiding storage of unnecessary zeros.

3. Implementing the Sparse Matrix Representation

A class was created to handle an NxN matrix as input. A function processed this matrix and converted it into the sparse format by:

• Iterating over all elements.
• Storing only non-zero elements in the structured array-stack format.

4. Computing the Determinant Using Cofactor Expansion

The determinant was calculated recursively using Cofactor Expansion. This involved:

• Choosing a row or column (typically the first row for simplicity).
• Expanding along that row:
  • Multiplying each element by its cofactor.
  • Recursively computing the determinant of the smaller submatrix (minor).
• Applying the (-1)^(row + column) rule to alternate signs.

5. Handling Sparse Properties in the Calculation

If an element was not found in the sparse structure, it was assumed to be zero, allowing for skipping unnecessary calculations. This optimization significantly improved efficiency, as operations were only performed on non-zero elements.

6. Solving for the Determinant

The recursive function computed determinants by reducing the problem to smaller submatrices. The program outputted the final determinant of the sparse matrix.